Silicon spin qubits
Spin qubits are one of the prospective types of qubit for future scalable quantum computers. However, reliable fabrication of these basic quantum elements is challenging and requires nearly perfect materials and nanometer precision owing to their small size and sensitivity to the electromagnetic environment. Silicon, which has been the material of choice for classical computing for many years, also has highly desirable properties for the fabrication of spin qubits.
Individually confined electron and hole spins in silicon-based quantum dots have been shown to have exceptionally long lifetimes, up to seconds or longer for electrons in isotopically purified 28Si. Thanks to the tremendous advancement of silicon technology in recent years, reliable fabrication of silicon quantum dots has come within reach. Some of the silicon transistor devices in the latest technology nodes can actually be used directly as spin qubits.
Why Quantum Computing
Technological progress goes hand in hand with incessant advances in computing power. Modern personal electronic devices have the computational power of a supercomputer from just two decades ago. Computer-aided designs, logistics, data analysis and cognitive computing have become an essential part of modern life. However, current progress in down-scaling transistors reaches physical limits when approaching atomic scales, and heat dissipation becomes a severe issue with increasing transistor densities.
Above all, certain complex physical problems such as computing energy spectra, correlations or time dynamics in molecular and condensed matter systems are beyond the reach of classical computers. These computations require exponential resources. The reason for this is the exponential growth of state space with the number of particles, preventing the computation of systems with more than a modest number of 50 particles. With a few more particles, even future supercomputers are destined to fail in performing exact calculations.
In contrast, a quantum computer has the potential to compute ground-state energies, energy spectra, time dynamics and correlations of such systems efficiently. Moreover, it is expected that certain types of optimization problems with application in logistics, time-scheduling and others can be solved more efficiently with the help of quantum effects.
Spin Qubit Technology
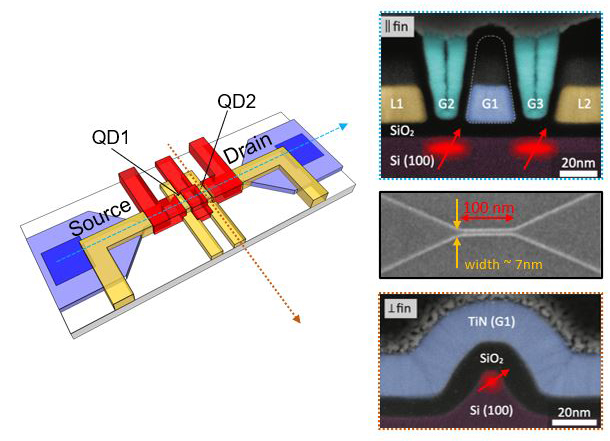
We focus on the bulk silicon FinFET platform as a basic element for qubit implementation. In conjunction with silicide based ohmic contacts this platform allows implementation of both electron and hole spin qubits in the same devices simply by changing the applied gate voltages. Lateral confinement in the fin reduces the gate complexity and allows the use of self-alignment techniques for smaller and more tunable devices.
Fabrication and Characterization
Fabrication takes place in our research scale cleanroom (the Binnig and Rohrer Nanotechnology Center or BRNC) which houses all the necessary tools for standard CMOS fabrication and advanced nanotechnology. The BRNC provides a cutting-edge, collaborative infrastructure designed specifically for advancing nanoscience. It hosts 950 m2 of cleanroom space and high-end e-beam and transmission electron microscope facilities. We are also collaborating with other IBM facilities around the world that host research scale pilot lines and more industrial cleanroom environments.
Controlling spin qubits
To use the spin of an electron as qubit, a long spin lifetime and the ability to manipulate the spins quickly and controllably are needed. These two requirements are difficult to meet simultaneously. For example, we can control spins with an electric field by using spin-orbit interaction. However, this makes spins susceptible to charge noise. We investigate spin coherence in semiconductor quantum dots and ways to manipulate the spins without compromising their lifetime. Such manipulation can be achieved in different ways, for example through spin-orbit interaction, magnetic field gradients or hyperfine interaction to nuclear spins.
Spin-orbit interaction in semiconductors
If electrons are moved in a semiconductor material where a spin-orbit interaction is present, the polarization direction of the electron’s spin rotates. In comparison to III-V semiconductors, the spin-orbit interaction for electrons in silicon quantum dots is weak. However, the spin-orbit interaction for holes is large and enables rapid spin manipulation using resonant electric field modulations.
Controlling noise in semiconductor spin qubits
The spin of an electron can be very well decoupled from the environment, making it an ideal qubit. This is because electric fields do not directly interact with electron spins. Magnetic noise arising e.g. from fluctuating nuclear spins of the host semiconductor and, in presence of spin-orbit interaction also electric noise can significantly decrease the spin coherence time.
More than 92% of the host material silicon consists of the spin-free isotope 28Si, reducing significantly magnetic noise. Through isotopic purification, the magnetic noise can be reduced further. We are working on schemes to get the remaining nuclear fluctuations under control. We also investigate techniques to reduce the influence of electrical noise by either reducing charge noise, or by implementing novel schemes to switch off the spin-orbit interaction.
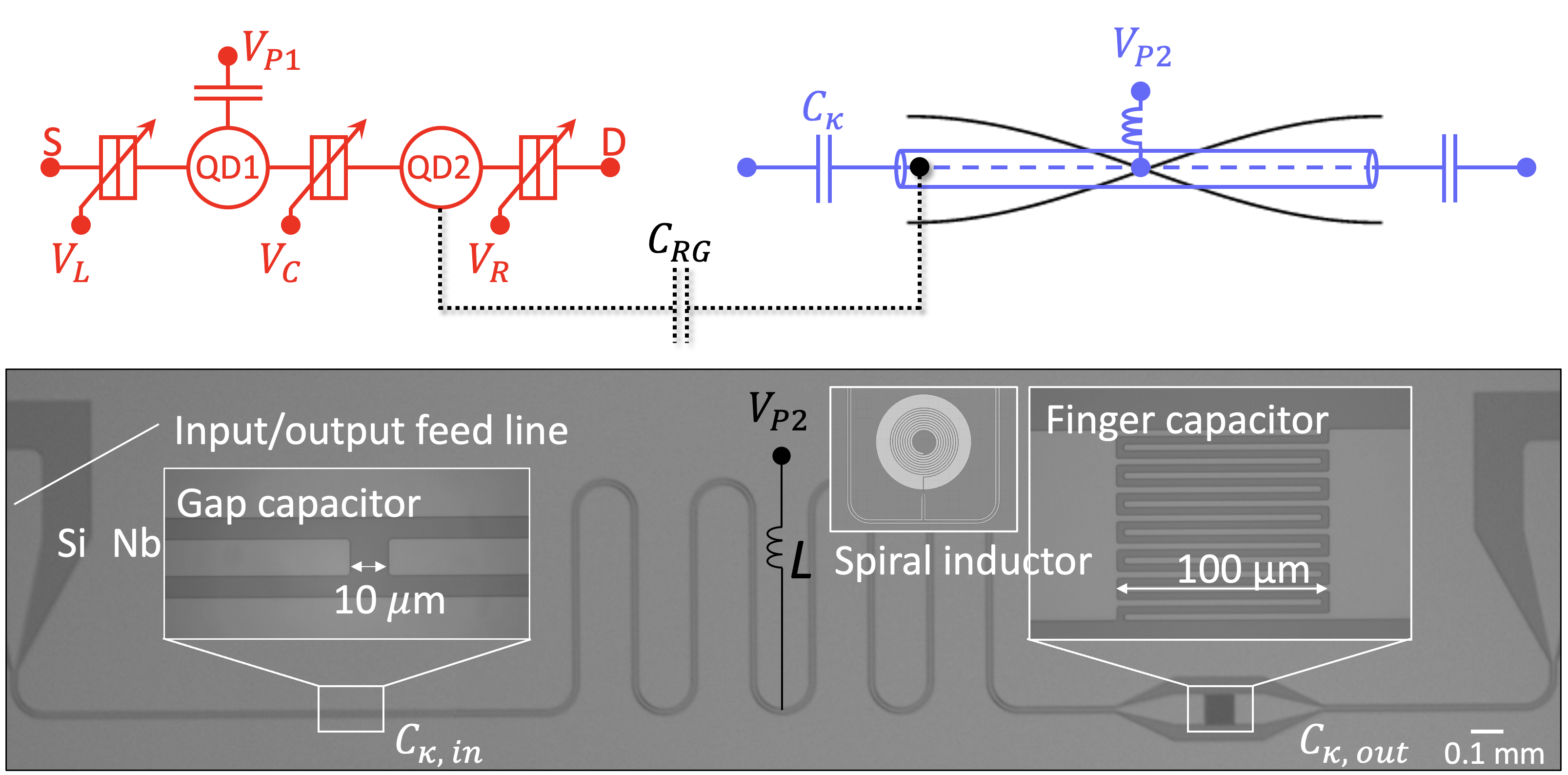
Read-out and coupling of remote spin qubits
Read-out of spin qubits requires a step of converting spin to charge. Charge read-out can be realized by coupling a gate of the quantum dot to a microwave resonator. Such resonators may also come to the rescue when facing the important but unresolved issue of long-range coupling of remote qubits. Such coupling can be an important ingredient in spin-qubit architectures since it may help to relax the wiring problem that arises when trying to electrically connect densely spaced quantum dots. We are addressing the coupling of spin qubits to superconducting microwave resonators, which is also linked to IBM’s more advanced superconducting qubit platform development.
Spin qubit fabrication
The cleanroom of the Binnig and Rohrer Nanotechnology Center gives us an ideal environment to explore new materials and fabrication methods and to develop chip designs for a scalable quantum computing architecture.
Ask the experts

Felix Schupp

Nico Hendrickx

Peter Müller

Eoin Kelly

Leonardo Massai

Michele Aldeghi