.png)
Quantum Threat and Quantum-safe Migration
Helping businesses to migrate to quantum safe cryptography
Tokenized Financial Asset Exchange
Building the platform for secure central bank digital currencies (CBDC)

Adversarial Robustness Toolbox
Securing AI models with the Adversarial Robustness Toolbox

Zero-knowledge Proofs
Advancing a core building block for privacy-centered cryptography

Functional Encryption
Building functional encryption from the ground up

Number Theoretic Cryptography
Develpoing elliptic curves, isogenies and more
Quantum-safe Cryptography Algorithms
Designing, implementing, and standardizing new quantum-safe cryptographic algorithms

Privacy-preserving Biometric Authentication
Cryptographic protocols for human authentication and the IoT

Fabric Private Chaincode
Enabling the execution of chaincodes using Confidential Computing

Lattice-based Cryptography
Using geometry of numbers to construct security primitives

Self-Sovereign Identity
Self-sovereign identity as an important enabler of civilian and enterprise identity use-cases

System Security
Using different methods to prevent systems from bein exploited

Automation and Reasoning in Threat Management
Helping security teams to manage cyber threats

Quantum-safe Systems
Designing a portfolio of high-security quantum-safe cryptographic services

Highly Resilient Transaction Processing
A highly resilient and high-throughput transaction processing platform
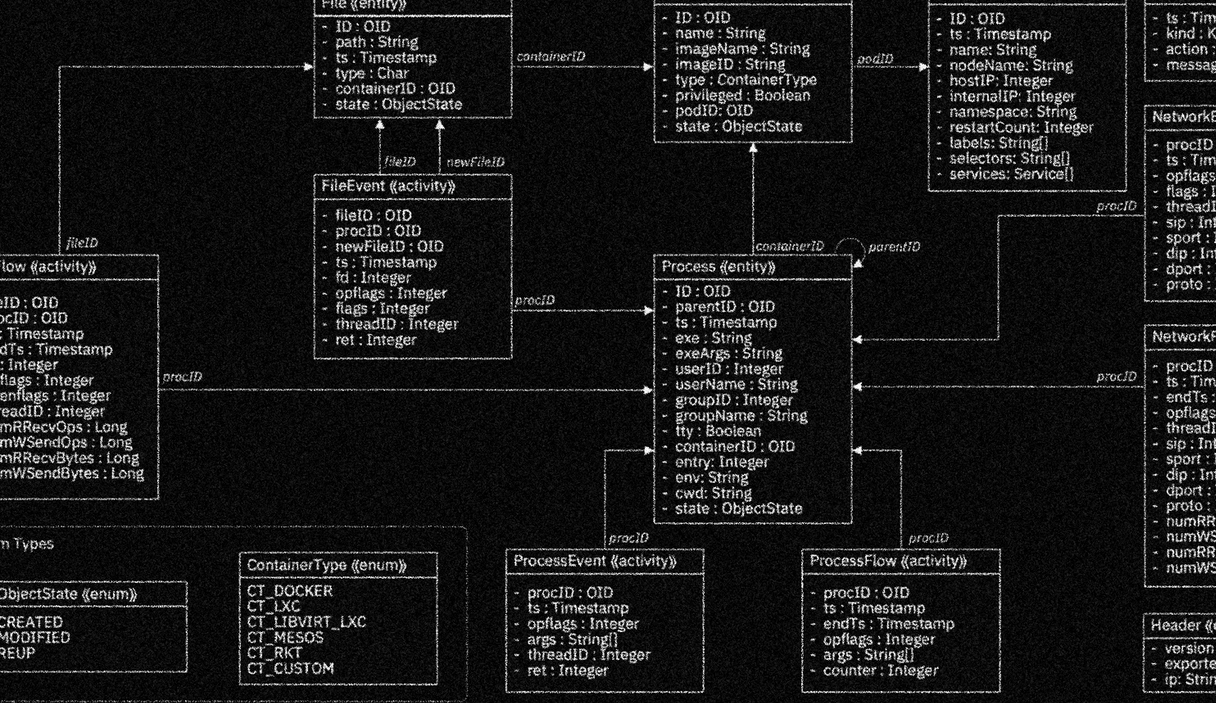
SysFlow
Enabling the creation of security analytics on a scalable, pluggable open-source platform
Crypto Anchors
Assuring the authenticity of products and assets
IBM Research Security Worldwide
At IBM Research, we research on many more topics related to Security & Privacy in our global labs. Learn more about our global strategy.
Join our team
We are currently looking for highly motivated and enthusiastic software engineers and researchers.
Contact

Marc Ph. Stoecklin
Principal Research Scientist
Head of Security Research